「人類史最高の発明は何ですか?」と聞かれたら何と答えますか?
たくさんあると思いますが、私は「数」ではないかと思っています!
人類史の中でこれまでに高度な文明がいくつも生まれてきました。
その背景にはかならず「数」の存在があります。
有名なエジプト文明では高度な数学が存在していたことがわかっています。
ピラミッド底面の正方形の辺の誤差は実に1/1000以下と非常に精巧に作られています。
この裏には高度に発展した測量術、数学があったと予測されています。
もしも「数」がなければ、お金が存在できず、物々交換でしか取引できなくなってしまうのではないでしょうか?
数詞に隠された歴史~N進法~
「口に出して数を数えてください」と言われたら
「馬鹿にしているのか?」と怒り出す人もいるかも知れません
誰でも止められない限りどこまでも数を数えられますよね?
でも、こんな当たり前のようなことも過去では、現在でも一部の地域ではそれができない、そういう概念がないことがあるのです。
数詞とは「数量や順序を表す言葉」のことです。
日本語で言えば、いち、さんとかで、英語ではone, twoなどと言った言葉です。
この数を表す言葉を言語ごとに見てみると面白いことが見えてきます。
日本語には、いち、にい、さん、よん・・・じゅう、じゅういち
と10まで行くと数字が繰り上がって10と1で11、12という数え方をしますよね
この10ずつひとまとめにして上の位に繰り上がっていく数え方を10進法と呼びます。
世の中には様々な繰り上がり方があって、それを「N進法」と読んでいます。
ひとまとめの仕方が10なら「10進法」です。
10進法では10は「底」と呼びます。
この当たり前のような10進法も実はつい最近までは統一されていませんでした。
その面影はいたるところにあります。
例えば、時計は1から始まって12で一回りする12進法が使われています。
また、角度は一周360°、一分は60秒など60を単位とした60進法は古代バビロニアで使われていました。
このように実はいろんなところに10進法以外の数え方が存在しています。
英語の数の数え方を見てみると
One, two, three, four, five, seven, eight, nine, ten, eleven, twelve, | thirteen, four-teen
のように12までは数の数え方に規則性がありません。このように英語には12進法の痕跡が残っています。
英語の国であるイギリスでは、例えば1ダースは「12」を意味する単位があります。12ダースは1グロス。
また、「長さ」では12インチが1フィート、通貨では12ペンスが1シリングというように12進法が色濃く残っています。
10進法が浸透した理由って?
10進法が浸透しているのは、人間の手指の数が「10」にあると考えられます。
手はいつも持ち歩いている?ので数えやすいですよね!
完全な10進法を生み出した最初の文明はエジプト文明と言われています。
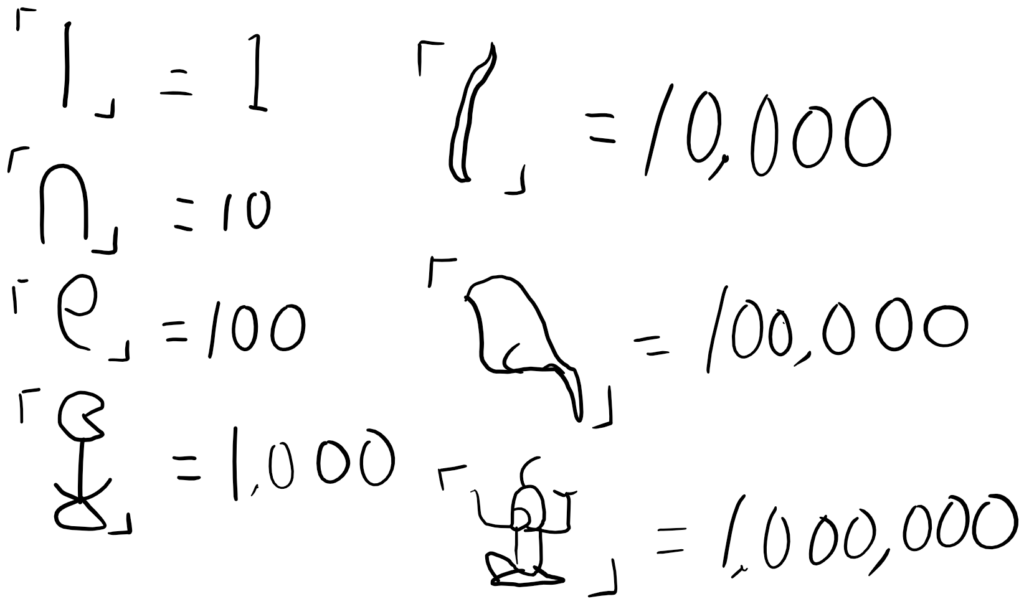
図1.古代エジプト文明で使われた数詞
エジプトでは、1千万まで数詞があったと言われています。
古代エジプトが数詞を使い回さずにたくさん生み出していたのは草の繊維で作ったパピルスに細かい字を書くことができたからだと考えられています。古代メソポタミア文明が起こったバビロニアなどでは、石、粘度に文字を書くために精巧な文字を書くことができません。
なのでくさび形文字など直線を多用した簡単な文字が使われ、数詞も繰り返し使用して節約していたと考えられてます。

図2.古代バビロニアで使っていた数詞
数を節約するという考えは実は数学の発展に重要でした。後にインドで発明される「0」の活用に繋がります。
10進法に慣れてる私達にとっては便利で、感覚的にもわかりやすいですが欠点もあります。
それは「分割」が苦手ということです。
10の約数(割り切れる整数)は「1,2,5,10」の4つと少ないです。生活でよく使用する、3や4などで割り切れないことが不便です。それに対して12進数は「1,2,3,4,6,12」の6つと多いので、分割に有利と考えられます!
このように「N進法」にはそれぞれ、利点や欠点が存在しています。
南米にいるある部族は1という数詞しかもっていないそうです。
また、オーストラリアの部族は2をひとまとめにした2進数を使っていたそうです。
2進数の考え方の始まりとされていますが、このように2までしか数えられないというとすごく幼稚なような気がします。
しかしこの0と1で表される2進数は現代でとても重要です。
それはコンピューターの世界では2進数を使っているからです。
機械にとって電流が「流れる」と「流れない」を0と1として処理する方法はシンプルで処理しやすく、高速に計算することが可能だからです。
このように見てみると数の発明からその数え方というシンプルな概念ですが、現代の発達した文明に必要不可欠ということが見えてくるようになってくると思います。
数字は人に説明する上でもとても重要です。ビジネスの世界でも納得感、説得力を出すには「数字で語れ」と言われたり、科学の世界でも、評価、証明には数字が非常に重要になってきます。これと比べると大きいとか、こっちよりもよく効くとかではなく、それを数字で説明することが求められます。
どうですか?「数」に興味が湧いてきませんか?



