平均変化率は微分の基礎となる重要な概念です。
「平均変化率」と聞くと難しい気がしますが、実は身近に接している概念です。
例えば、車で走行したら1時間後60km進んでいました、このときの平均時速は60km/hですが、この時速がまさに平均変化率の一例です。
微分は物理学や統計解析、機械学習などを理解するためにも重要ですので概念を理解していおくと役立つかもしれません。ここでは人工知能を使いこなすための基礎数学として微分を中高レベルから復習していこうと思います。
 こめやん
こめやん
平均変化率って何?
平均変化率は「時間変化」をイメージするのがわかりやすいです。
例えば「平均睡眠時間」を計算してみます。
とある3日間の睡眠時間が5時間、4時間、6時間でした。
一日あたりの平均睡眠時間は何時間でしょうか?
答えは簡単ですね(5+4+6)時間÷3日間=5時間/1日です。
各日の睡眠時間がバラバラでも3日間集計して日にちで割れば「一日あたりの平均睡眠時間」がわかります。平均変化率を求める時もこれと同じようなことをやっています。ちなみにグラフをとってみます。
x軸を日にち、y軸を睡眠時間としたとき、平均睡眠時間をグラフに表すとy=5xになります。これは一次関数と呼ばれるもので、変化の仕方が常に一定であると言う特徴があります(だから直線)。
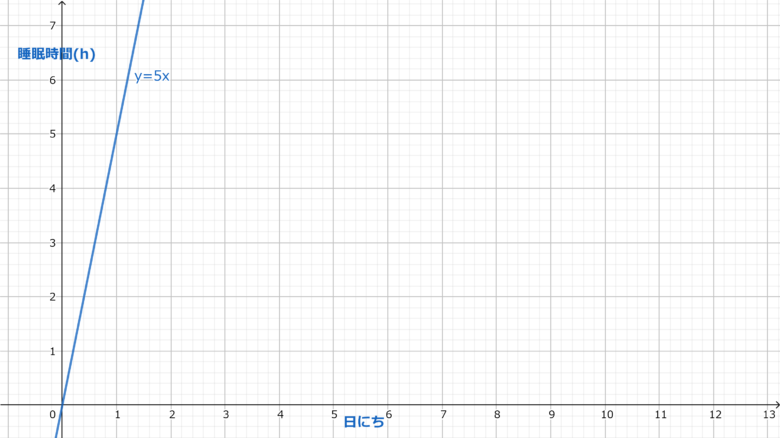
一次関数y=5xにおいて、xの値を0から2まで変化させたとき、yは0から10に変化します。このときのxの変化に対するyの変化の割合を求めると
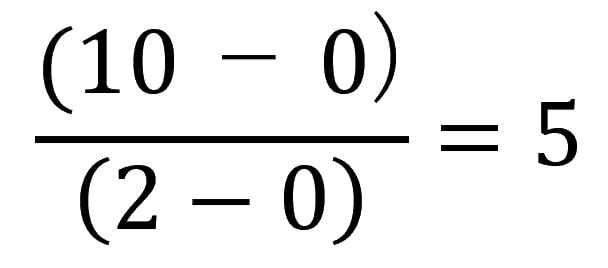
です。この5がxの値が0→2まで変化させたときのyの平均変化率です。一次関数はどこのXの区間を取っても平均を求めたら5になります。
 こめやん
こめやん
二次関数などの変化率を考えていくと面白くなってきます。
平均変化率と微分係数の違い
二次関数での平均変化率
この平均変化率を二次関数で考えてみましょう。
二次関数の代表例として物体の自由落下を取りあげます。
y軸を距離[m]、x軸を秒数とします。
物体が垂直に落下したときの時間と距離の関係は以下の式のようになります。
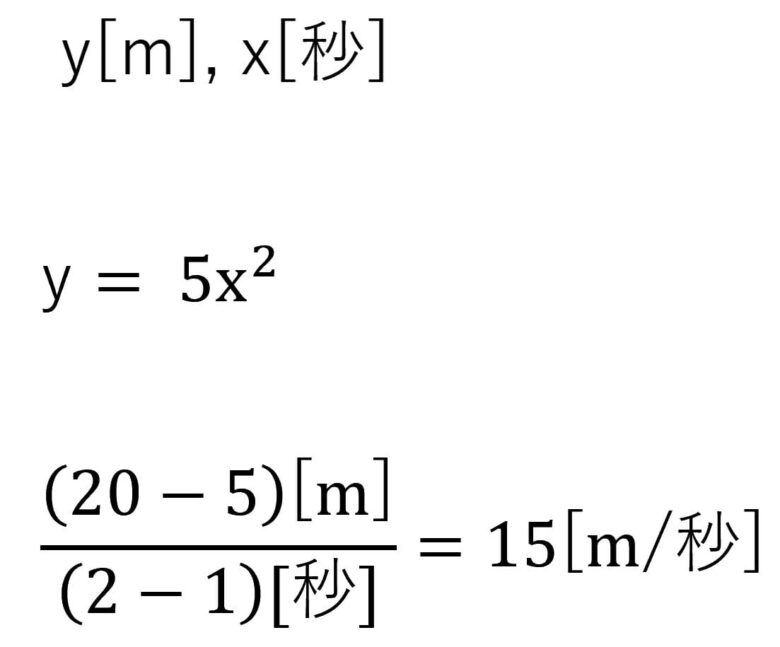
この二次関数の1→2秒におけるyの平均変化率は上記のように15m/sになります。
また、0→1秒におけるyの平均変化率は、(5-0)/(1-0)=5[m/s]になります。
 こめやん
こめやん
 adeno
adeno
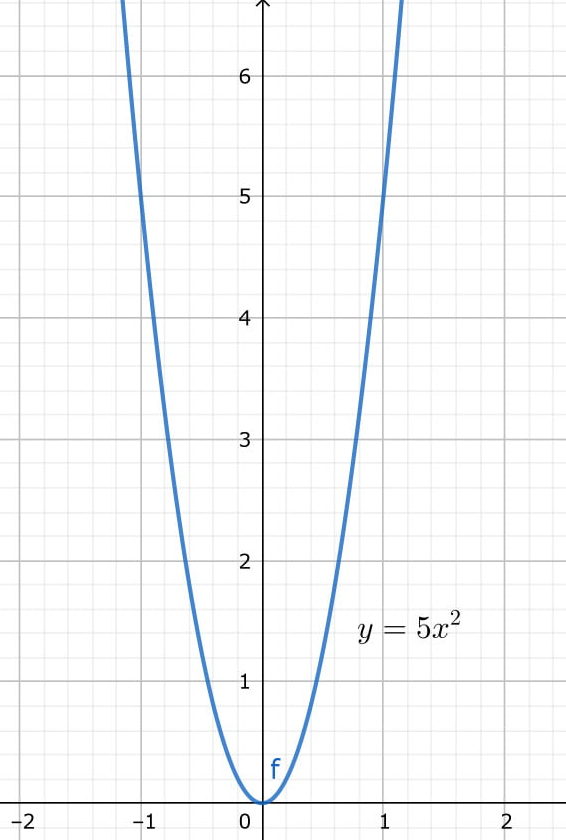
このように一次関数とは違って二次関数では平均変化量は測定する区間によって変化します。
瞬間の速さと極限
瞬間の速さと言う表現があります。平均ではなく、その時間の時の瞬間の速さです。
一次関数では常に同じスピードなので迷う必要はありません。
それでは二次関数の瞬間の速さはどのように求めるでしょうか?区切る時間によって速さは変化してしまいますよね?
 こめやん
こめやん
限りなく短い時間(0.00..1秒)の時間の変化を見れば瞬間の速さに近い値がわかります。
 こめやん
こめやん
 adeno
adeno
では時間を短くしていくと変化率にどのような変化が起こるか見てみましょう。
1.98秒→2.00秒における距離の平均変化率は(20-19.602)[m] ÷ 0.02[秒]=19.9m/s
1.99秒→2.00秒における距離の平均変化率は(20-19.8005)[m] ÷ 0.01[秒]=19.95m/s
1.99999 → 2.00000秒における距離の平均変化率は (20-19.9998000005)[m] ÷ 0.00001[秒] = 19.99995 m/s
 こめやん
こめやん
 adeno
adeno
瞬間の平均変化率
それではこの限りなくある時間から、先ほどの限りなく短い時間のあいだの変化、瞬間の平均変化率を見てみましょう。
数学っぽく瞬間の変化率を文字式を使って表してみましょう。
 こめやん
こめやん
関数はf(x)=5x2。ごく短い時間をh秒としたとき、2秒-h秒(1.999秒のような値)から2秒にいたるまでの平均変化率を先程と同じように計算します。
 こめやん
こめやん
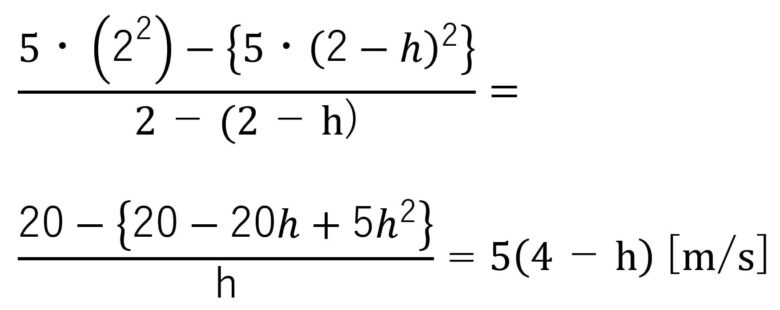
ここでは瞬間の変化率を求めたいので、h秒は0に限りなく近い値に設定します。
hが限りなく0に近づくと-5hは0に近似します。よって ≒20m/sとなります。
このようにhを限りなく0に近づけた時に平均変化率は限りなくある値に近づきます。この値を極限値とよびます。
(2-h)→2秒のように1.999秒→2秒の平均変化率を見ましたが、2秒→(2+h)として、2秒→2.00…1秒の平均変化率をみてもどちらも2秒における瞬間を見るという点では同じです。この計算を解くと5(4+h)となり、hを限りなく0に近づけると同様に20m/sに限りなく近づきます。
limの読み方と表記の仕方
hがある値に限りなく近づくことを表現するには「lim」を使います。
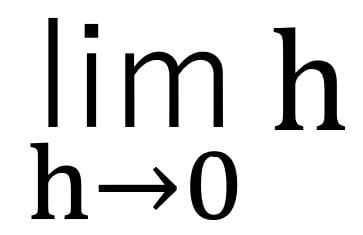
これは、「hを0に限りなく近づける」という意味です。この式は「hを0に近づけたときのhの極限」を表しています。hが関数:f(x)や0が無限大:∞であるときもあります。
「lim」は英語でlimit:極限の意味です。
この式の読み方は、英語でも日本語でも決まっておらず、人によって読み方が異なるようです。 Limit as h approaches 0 あるいは limit of h as h goes to 0 などと読みます。
日本語では英語読みすると長くなるので、「リミット hを0」などと読むようです。
平均変化率と微分係数
長い期間ではなくごく短い瞬間の変化率が微分係数になります。
これ以上細かくできないほど微細に分けること→微分というようなイメージです。
文字式をつかって一般化してみましょう。
関数f(x)のとき、xがaからbまで変化するとf(x)はf(a)→f(b)に変化します。つまりf(x)の平均変化率は、f(b)-f(a) ÷ b-aです。
aからbまでの変化をごく短い時間h経過後の変化は a→a+hとします。すると上の式の「b」は「a+h」になります。hを0に近づけると極限値が求まります。
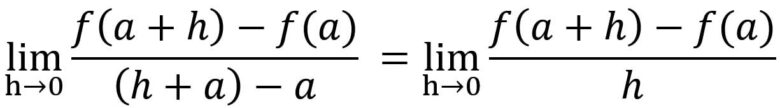
関数f(x)に対して、極限値 f’(a)をx=aにおける微分係数といいます。
(公式1) f(x)のx=aにおける微分係数は
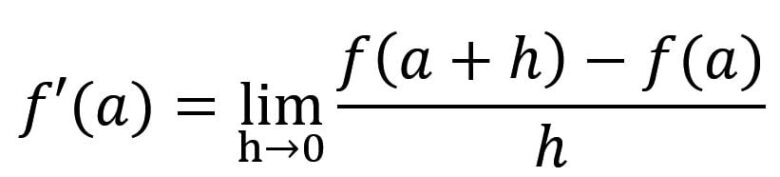
微分係数はxの値によって変化します。これをaのような固定の値(2とか5とか)としてではなく、様々な値を取る変数 xで微分したものを導関数といいます。
f(x)=5x2の導関数を求めるとf'(x)=10xとなります。
 こめやん
こめやん
微分係数はf(x)の接線の傾きになる
f(x)=5x2のとき、導関数f'(x)=10xです。
このときx=1のときの微分係数はf'(1)=10です。
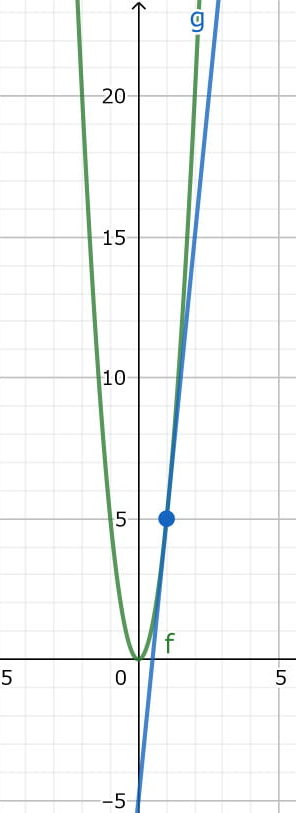
関数f(x)を通る接線の傾きが微分係数になります。接線とはf(x)上の点だけを接するように通る線です。
接線の座標はf(x)=5x2上の点なのでx=1を代入して(1, 5)になります。
二次関数を通る接線は 微分係数10を傾きとなる1次関数なのでy=10x+bです。
座標を代入するとb=-5なので点(1,5)を通る接線の方程式はy=10x-5です。
極限で使うhの意味
極限値を表す式では、hを文字として利用しますが、これには意味があるのでしょうか?
結論から言うと、hがなぜ使用されているかは不明です。とりわけ「h」が何かの頭文字というわけでは無いようです。
極限値を表す数式のなかでhが使われるようになったのは、19世紀です。
18世紀最大の数学者と名高いラグランジュおよびその業績を書としてまとめたラクロワは「h」を使用していたようです。
オームも1829年に出した論文中でhを使用しています。
その一方で1850年代複素解析で有名なフランスの数学者コーシーは「h」ではなく「i」を使っていたようです。
iは「increment:増加」を表す頭文字として数列などでもよく利用される頭文字であるため、hに変更されたとする見方が多いようです。
 こめやん
こめやん
微分の記述法
微分、導関数の記述法にはたくさんあって混乱することもあるとおもいます。
よく利用される関数f(x)の導関数f'(x)という記述方法はラグランジュの記法です。
またd/dxの記法はライプニッツの記法です。
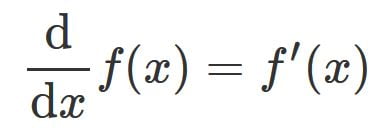
物理ではニュートンの記法といって関数yに対して上に「・」をつける記法もあります。