定量下限と検出限界 (limit of detection) 高感度な検出法とは？

分析手法は確立されているものだけではありません。自分で新しく分析手法を開発した場合はその計測値が妥当なものか？を確認する必要があります。特に様々な値の中から意味のある値を検出する分析手法では妥当性を確認する事項がたくさんあります。

妥当性を確認するためには、「精度(繰り返し精度)」「確度」「再現精度」「特異性」「検出限界」「定量限界」「直線性(検量線)」「ダイナミックレンジ(定量範囲)」「SN比」などがあります。

この記事ではどこまで微弱なレベルの測定ができるのか？分析手法の限界を評価する指標である「検出限界」と「定量限界」について紹介します。

検出限界 (LOD: limit of detection)

検出で「シグナルが検出できなかった」という時、分析方法として「定量性のある範囲から外れた値であたるからできない」とするのか「全くシグナルが得られなかった」というのでは意味が異なります。

検出限界は定量性があるかどうかはさておき、「電気信号として検出することができる最小量のこと」です。

定量下限 (LOQ: limit of Quantification)

一方で分析手法としては、分析値を二者間で比較したりするため定量性が重要になります。

定量下限は定量可能な最下限の値を表します。この定量下限は検出加減よりも大きな値をとります。

検出下限と定量下限の求め方

まずは計測値の平均や不偏標準偏差に対する考え方

とある分析手法でシグナル検出した時に、n=6回の検出値が10.102, 10.151, 10.332, 9.998, 10.354, 10.245と出てきました。

まずこの値の平均値と標準偏差を求めましょう。

平均値は10.197です。

この感覚を図示すると下の図のようになります。中央を平均値として園周辺の値が測定される確率が最も高く、その値からプラス(→)、マイナス(←)に均等に測定される確率が急激に下がっていきます。このような確率の分布を統計学的に正規分布と呼びます。

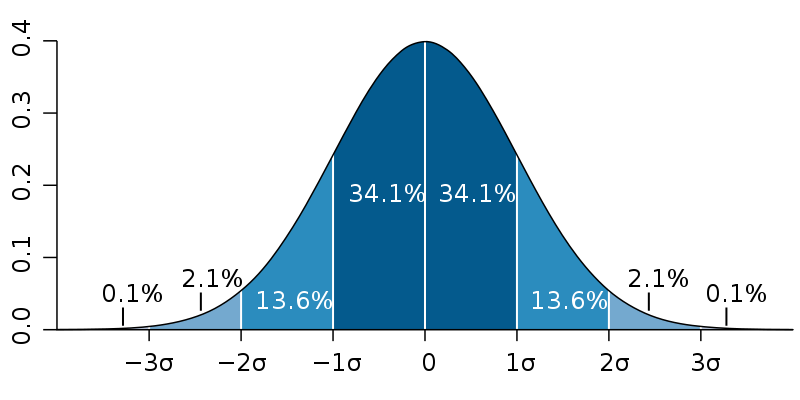
正規分布と標準偏差の関係 from M. W. Toews [CC BY 2.5 (https://creativecommons.org/licenses/by/2.5)]

これを求めると0.139になります。この標準偏差は測定値のばらつきの大きさを表します。平均値と合わせるて表記すると10.197±0.139です。

もう一度上の正規分布の図を見てください。

この正規分布は平均値を中央とした時に山なりに左右対称な分布を持っており、標準偏差±1σの範囲に測定値の約68.2%、±2σに約95％、±3σに約99.7%が入っているといえます。

言い換えると±3σに99.7%の測定値が収まるなら10.197±0.417→9.78未満と10.614を超えの値が出る確率は約0.3%だということです。9.75や10.617が出るのはかなり珍しいと言えます。

検出限界はブランクまたはバックグラウンドの±3σ

水に溶かした成分Aを吸光度で測定することを考えます。

このとき水には成分Aは当然含まれていません。これをブランク(バックグラウンド)とします。

成分Aが溶けた水には成分Aが含まれていて吸光度を測定すれば、何らかの値が出てきます。

例えば、10 mMでは吸光度0.6、5 mMでは吸光度0.3のように濃度を落とせば比例的に吸光度が低下します。得られた値を使って下の図左のように検量線が引けます。

しかし、検出にも限界があるので、濃度を下げていくとある一定の濃度からは変化がわからなくなって来るはずです。

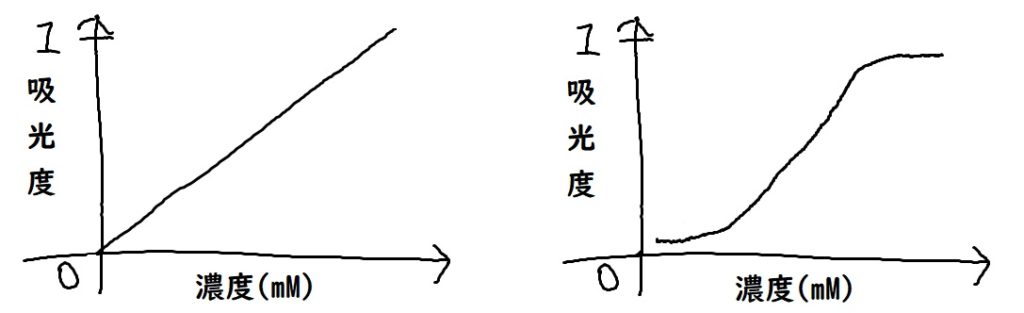
検出限界：左は理想。右は現実。濃度を落としていけば有る濃度以降は吸光度の増減が緩やかになる。

そういう方法もありますが、逆の見方をします。先程の±3σから外れる値は珍しいという正規分布の考えを使います。

成分Aが入っていなくてもブランクの吸光度は0ではなく何らかの値が出てくるはずです。このブランクの吸光度も正規分布に従うはずです。

したがって、ブランクの平均値μと標準偏差を求めて、μ±3σを計算して、これから外れる値はかなり珍しいので((100-99.72)÷2=0.14%右側のみの確率)、意味がある値→検出できる吸光度・濃度だということです。

例えば、ブランクの平均値μ=0.1, 標準偏差σ0.02だった時、μ±3σ＝0.1±0.06となります。

つまり、吸光度の0.16を超える値は検出可能とみなします。この吸光度を検量線y=0.06xに当てはめると検出限界の濃度は2.7 mMになります。

3σを利用する考えはKaiserが1965年に報告した考え(H. Kaiser :Fresenius Z. Anal. Chem.,209,1(1965))ですが、現在はCurrieが提唱したよりリスクの低い方法として3.29σの値を検出限界とすることがIUPAC、ISOの方針になっています。

定量下限の求め方

先程の検出限界は検出ができるかどうか？ということに着目しているので、定量に関する信頼性をもっていません。

定量下限はより大きく幅をとって、ブランクの10σがよく使われています。定量に関する信頼性があるかどうかについては10σで十分かどうかについては検出手法によって変わるので吟味する必要があります。

例えば原子スペクトル分析での定量下限は√2×10σが使われます。

定量下限を正しく見積もるには、ブランクの測定結果が正規分布している必要があります。正規分布かどうかは「Shapiro-Wilk」や「Kolmogorov-Smirnov」などの正規性の検定により見極めます。

参考

1) 上本道久. “検出限界と定量下限の考え方.” ぶんせき 425 (2010): 216-221.