目次
演繹と帰納の語源
演繹と帰納はどちらも「りんご→赤い」とか「人間→必ず死ぬ」などといった「結論を導き出す方法」ですが、結論を導く根拠の結びつけ方が異なります。
演繹は一般論(前提)をもとに当てはめて一つの結論(仮説)を得る論理的推論法
帰納は個別の結果から一つの結論を見つける論理的推論法
 こめやん
こめやん
演繹と帰納の性質?のイメージをまとめると
- 演繹:簡単、当てはめて考える、「常識的に考えて…」
- 帰納:大変、規則性を見出す、「データから考えると…」
という感じです。
日常的に使っている推論はどちらかといえば演繹です。数学でピタゴラスの定理(一般論)に当てはめて直角三角形の斜辺の長さを求める(結論)のも演繹法です。帰納はデータを集める必要があるので大変ですね。
 こめやん
こめやん
「常識」のような普遍的な一般論に当てはめて結論づけるのが演繹法
個々のデータから規則・法則を導き出すのが帰納法です。
 こめやん
こめやん
演繹法の例
「鳥→空を飛ぶ」という一般論・常識を元にすると
カラスは鳥であるから、カラスは空を飛ぶと推論できます。同じく、すずめもオウムも鳥なので空を飛びます。

演繹法の例
演繹推論の弱点は、前提となる一般論が間違っている。あるいは例外があると間違った推論をしてしまうことです。
演繹法で誤った推論が導き出される例
例えば、ダチョウは鳥ですが、空を飛ぶことができません。演繹法で推論すると、ダチョウは鳥なので、スズメやオウムの例と同じく空を飛べるという誤った推論をしてしまいます。

演繹法の弱点 ダチョウのような例外に演繹法は弱い
演繹法は前提が誤ると結論も誤る
前提となる一般論自体が誤っているとそこから導き出した結論も誤ってしまうのが演繹法の弱点の一つです。たとえば、ただの偏見や先入観、古くからのしきたりなどをもとにした前提は客観的な検証がないために間違っている場合があります。
例えば、「美人→性格が悪い」「信仰が薄い→感染症にかかる」というようなものです。
美人は性格が悪いというのは偏見であり、それに当てはめて考えると誤った結論を導いてしまいます。
帰納法の例
帰納法は個々の事例から一つの法則性・共通性を見出して結論付ける方法です。
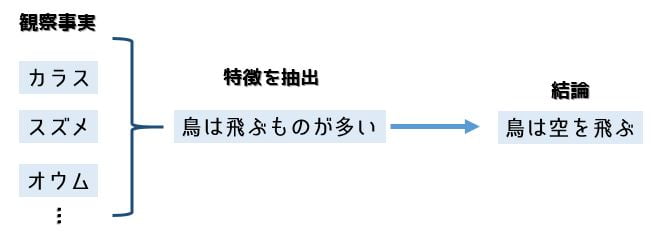
帰納法の例
帰納法の利点は観察事実を複数集めることによって、例外をきちんと把握できる点です。上の例に鳥でも飛べないダチョウが入れば、確かにダチョウは鳥類だけども飛べない例外もいるというように認識できます。
一方で帰納法の弱点は観察事実に対してバイアスがかかることです。例えば、自分の仮説に対して都合の良い観察事実だけに注目して集めてしまう確証バイアスがあります。
演繹法と帰納法は論理的推論の基本的な方法
これまでに登場した演繹法と帰納法は論理的推論法の基本的な方法の一つです。論理的推論法とは、論理的に推論する方法ー論理的に未知の事例に結論づける方法です。
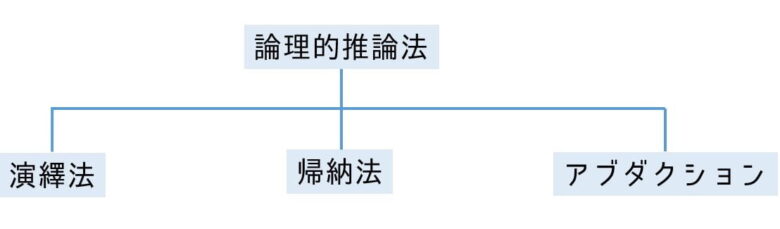
論理的推論法の例
推論とは?
物事を主張したり認識、理解したりするには理由付けが必要です。カラスが鳥だと理解しているのも羽が生えているのが鳥である。というような理由付けが行われているからカラスは鳥であると主張したり、理解できています。

未知の情報、事例に対して理由付けを行って結論づけることを「推論」といいます。しかし「かさかさしているものは虫」とか「羽が生えているものは鳥」というように適当な結論の出し方では誤った認識をしがちです。
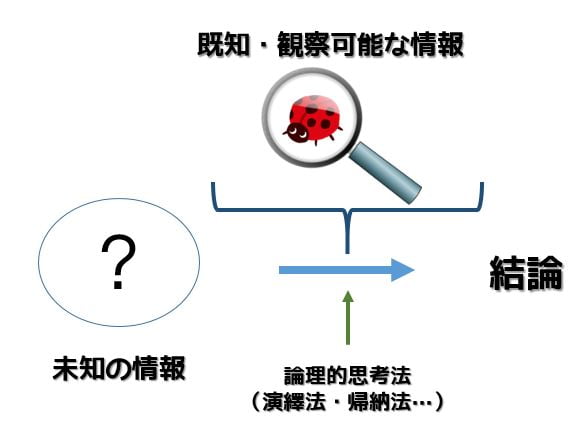
論理的推論とは?
論理的推論は演繹や帰納など論理的思考法にのっとって推論する方法です。
[chat face=”komeyaniro.png” name=”” align=”left” border=”gray” bg=”none” style=””]論理的推論をしても間違いはありますが適当よりかはましです[/chat]
演繹法と帰納法の流れ
演繹法と帰納法では流れが違います。演繹法ではトップダウン型の流れで、一般理論や法則から始まって、仮説事例を当てはめて検証していって、結論を出します。
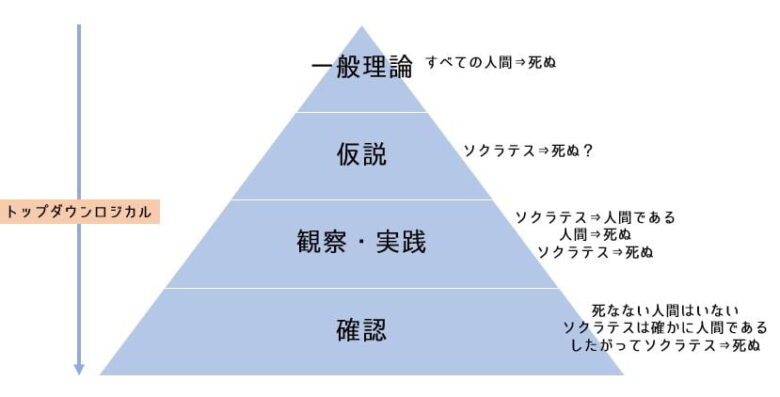
演繹法の流れ
一方で帰納法では、観察した事例からパターンを見つけ出して仮説、理論づけを行います。
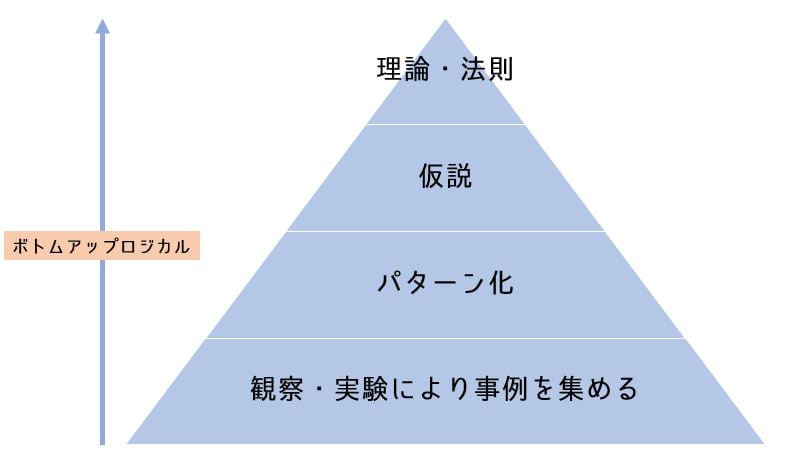
帰納法の流れ
 こめやん
こめやん
演繹と帰納の語源
演繹と帰納が直感的にわかりにくいのは漢字のせいだと思います。言葉から何を意味しているのか想像しにくいです。
演繹の語源は中国の思想家、朱子学を創始した「朱熹」の「中庸章句序」に登場した言葉と言われています。
演繹は「意義を推し拡げて説明すること」と説明されています。
「演」は訓読みでは「のべる(演べる)」と読み。ひきのばすとか説明するという意味があります(参考:デジタル大辞泉)。
「繹」は訓読みで「たずねる(繹ねる)」と読み。糸を引く動作を意味していて「糸口を引き出す」という意味があります(参考:デジタル大辞泉)。
 こめやん
こめやん
帰納の語源は西周という日本人の哲学者が帰納の英訳「induction」を和訳したことで生まれたようです(wikipedia日本語版:西周)
「帰」は有るべき場所に帰って納まる。という意味があることから、
様々な個々のデータが一つの法則に帰って納まるという意味が帰納にあるのでしょう。



